דיאגרמת משוב סיבתי (Causal Loop Diagram)
דיאגרמת משוב סיבתי (מאנגלית - Causal loop diagram או בקיצור CLD) הוא כלי מעולם החשיבה המערכתית אשר נועד לתאר את יחסי הגומלין בין המרכיבים השונים במערכת ומסייע לנתח את הסיבות למציאות הנוכחית, לזהות תופעות מתהוות ולגבש נתיבי השפעה על הדפוסים במערכת. דיאגרמת משוב יכולה להיות כלי ליצירת הבנה וכן כלי מתמטי שמאפשר בניית מודל.
הדיאגרמה מחברת שלושה נדבכים שהם בעלי ערך רב להבנה של מערכות:
- סיבתיות - הדיאגרמה מבקשת לחשוף את הסיבות למציאות הנוכחית במערכת, ואת דרכי ההשפעה האפשריות לקידום שינוי. הנחת המוצא היא שהסיבות לתופעות שאנו חווים אינן ברורות, ולכן יש צורך לחשוף אותן.
- משוב - הקשר בין המרכיבים והתהליכים השונים במערכת מייצר מעגלי משוב שמעצימים או מחלישים תופעות מסויימות. הסיבתיות המעניינת היא זו שמועצמת או נחלשת במהלך הזמן, ואלו בדיוק נקודות ההתערבות הרלוונטיו.
- דיאגרמה - המודל מאפשר להציג באופן ויזואלי יחסי גומלין מורכבים. ההבנה הויזואלית מסייעת לנו מאוד להבין מורכבות ותהליכים לא לינאריים.
הרעיון של מעגלי משוב מאפשר לנו לייצר תיאור מערכת על בסיס המעגלים החיוביים והשליליים שמתקיימים במערכת. באופן זה ניתן לתאר ״מעגלי קסמים״ בתוך המערכת ולפתח כלים לשיפור של מעגלי המשוב החיוביים, ולצמצום או קטיעה של מעגלי משוב שליליים.
מה יש בדיאגרמה
דיאגרמות משוב מורכבות מהמרכיבים הבאים:
- רכיבים ותהליכים - הדיאגרמה מציגה את המרכיבים של המערכת, ברמת השחקנים, ארגונים, קבוצות וכדומה. בנוסף לרוב מוצגים תהליכים מרכזיים גלויים מרכזיים באותה רמה.
- זיקות - הקשרים בין המרכיבים והתהליכים השונים מיוצגים באמצעות קווים המחברים ומתארים את ההשפעות השונות.
- טיב הזיקות - הדיאגרמה מבקש לתאר את איכות ההשפעה של המרכיבים אלו על אלו.
- לולאות משוב (feedback loops) - כאשר זיקה מסויימת משפיעה בחזרה על הגורם המשפיע נוצר תיאור למעגל משוב המתקיים במערכת. מתוכם יווצרו:
- לולאות מאזנות (blancing loops) - לולאות שמובילות למצב של איזון במערכת (למשל - גדילה של אוכלוסיית הטורפים מצמצמת את אוכלוסיית הנטרפים באופן שמצמצם את אוכלוסיית הטורפים ומוביל לאיזון לאורך זמן)
- לולאות מחזקות (reinforcing loops) - לולאות שמחזקות מגמה ללא איזון (למשל: עליית ריכוז הפחמן הדו-חמצני באוויר מוביל להתחממות שמובילה למדבור באופן שפוגע בצמחים המפרקים פחמן דו חמצני).
דוגמה: הקשר בין מספר הרכבים והפקקים
ניתן לייצג את הקשר בין מספר הרכבים על הכביש לבית מצב הפקקים באופן הבא:
ניתן להוסיף או להחסיר באופן דינמי רכבים או פקקים ולראות את ההשפעה על המצב השניה לאורך זמן (נוצר באמצעות Loopy)
מהדיאגרמה ניתן להבין כי ככל שיש יותר רכבים יש יותר פקקים, אבל ככל שיש יותר פקקים אנשים יטו לקנות פחות מכוניות או לנסוע פחות ולכן יש לולאת משוב מאזנת. אבל ברור לנו שחסרים רכיבים קריטיים בתיאור המערכת הזה. לכן נרצה להוסיף הקשר בין מצב הפקקים להשקעה בכבישים, בין צמיחה כלכלית למספר הרכבים ובין מצב הפקקים ליצירת חלופות לרכב פרטי (למשל - עבודה מהבית, תחבורה ציבורית וכיוב׳). במצב כזה תווצר לנו מערכת יותר מורכבת:
ניתן להוסיף באופן דינמי כל רכיב במערכת ולראות את השפעות על הגורמים האחרים לפי טיב ההשפעה (נוצר באמצעות Loopy). ניתן לראות שכמעט בכל מצב במציאות הנתונה הפקקים אינם מתמעטים. עם זאת, לעתים הכנסה של גורם אחד עשויה לצמצם דרמטית את התופעה הבלתי רצויה. (למשל מעבר לרכבים אוטונומיים).
התיאור הנ״ל כבר מתאר את המציאות הכאוטית של המערכת. מאחר והתיאור אינו כולל את חוזק ההשפעה, קשה להגיע למסקנות מספריות מהמבנה הזה, אבל ברור שהמענה בתחום אחד (למשל - סלילת עוד כבישים, מיסוי על רכב וכיוב׳) לא יכול לספק מענה מערכתי. תיאור זה מבהיר מדוע התחבורה היא בגדר בעיה סוררת.
תהליך יצירת הדיאגרמה
תהליך היצירה של דיאגרמת משוב אינו לינארי, אבל מחייב מיקוד במספר מרכיבים שונים שתוארו לעיל. מספר דגשים ליצירת התהליך (אלו לא חייבים להופיע בהכרח בסדר הזה, וניתן בכל שלב לחזור ולשנות את המרכיבים הקודמים בהתאם להבנות):
- ניסוח גבולות המערכת - לנסות להגדיר מה מצוי בתוך תחום המערכת שלנו (על בסיס מידת החיבוריות וההשפעה בין המרכיבים השונים) ומה משפיע מבחוץ או כלל לא משפיע (ולכן לא יוצר בדיאגרמה).
- השחקנים והתהליכים המרכזיים בתוך גבולות המערכת - הצבת השחקנים והתהליכים המשפיעים על הסוגיה הנדונה
- שרטוט הזיקות הבין השחקנים - שרטוט מערך הקשרים בין השחקנים והתהליכים (בקווים המחברים בניהם)
- תיאור טיב הזיקות - יש להגדיר האם ההשפעה היא חיובית או שלילית.
- זיהוי מעגלי משוב - בחינת ההשפעות המעגליות, וסגירת מעגלים שפספסנו בשרטוט הזיקות
- תיוג מעגלי משוב מאזנים ומחזקים - בשלב זה נסתכל על המעגלים שנפרסו ונתייג אותם כמעגלי משוב מאזנים או מחזקים.
איך נייצר דיאגרמות אפקטיביות
כדי לבנות דיאגרמות אפקטיביות רצוי לתת את הדעת להיבטים הבאים:
- שימור הגמישות בתהליך - מאחר ואנחנו מנסים לתאר את מערך הקשרים בין מגוון הגורמים, יש לשמר גמישות של המפה המתהווה. לכן כדאי לעשות שימוש באמצעים דינמיים: פתקי פוסט-איט, כלים וירטואליים, לוח מחיק וכיוב׳ מאחר ונדרשים לא מעט שינויים והתאמות במעלה הדרך.
- התהליך לא פחות חשוב מהתוצאה - התהליך של יצירת הדיאגרמה הוא חלק משמעותי מהערך שלה בחשיפה של הסיבתיות הסמויה.
- כל זיקה מחייבת הסבר איכותי, לפחות בע״פ - מאוד קל למתוח קווים, יותר קשה להסביר את טיב הזיקות. לכן יש להתעקש על תיאור כל זיקה. את התיאור רצוי לתעד, והוא חלק מהתוצרים של המפה, גם אם קשה להציג אותו ישירות על גביה.
- התכלית היא היגיון, לא שלמות - המטרה של המפה היא לא לייצג את כלל הזיקות (ככל שהמערכת גדולה או מורכבת יותר זו נעשית משימה בלתי אפשרית) אלא לייצר הבנות והגיונות חדשים. לא פעם כדי לייצר היגיון אנחנו נבקש להשמיט ביודעין חלקים מהמפה שמכבידים על ההבנה. בדומה, אם נוכל להשתמש בכלים שיסייעו להבהרת התמונה (צביעה של שכונות מסויימות, תיאור צמתי מפתח וכיוב׳) כדאי לעשות זאת למרות שזה לא חלק מהאפיון הבסיסי של דיאגרמות משוב.
- ניסוח התובנות - לאחר ששירטטנו את הדיאגרמה כדאי לשאלות מספר שאלות שיסייענו לנו להבין את המערכת טוב יותר:
- אילו דפוסים נחשפו במפה? נסו להמשיג אותם.
- אלו שחקנים או תהליכים לא מאוד משמעותיים בהשפעה שלהם למרות שהם כן מוצבים על המפה?
- אילו זיקות קריטיות לקידום ההשפעה הרצויה וכיצד נשפיע על זיקות אלו?
- את מה לא הצלחנו לייצג אבל לתחושתנו מטה את הכף לכיוונים מסויימים? (לרוב - היבטים תשתיתיים יותר קשים יותר לייצוג)
המגבלות של דיאגרמות משוב
דיאגרמות משוב מנסות לייצר תיאור ״מציאותי״ של המציאות הסבוכה במערכת. התיאור הזה מסייע מאוד ככל שהקשרים בין המרכיבים השונים נושאים קשר עובדתי (למשל הקשר בין אינטנסיביות הדיג ומצב הדגה) אך מתקשה לייצג תהליכים מורכבים הכוללים מודלים מנטליים אנושיים המשפיעים על המציאות. ככל שהמציאות הנבחנת מורכבת יותר המפה תהפוך למורכבת גם כן ובשלב מסויים היא תאבד את הערך ההסברי שלה.
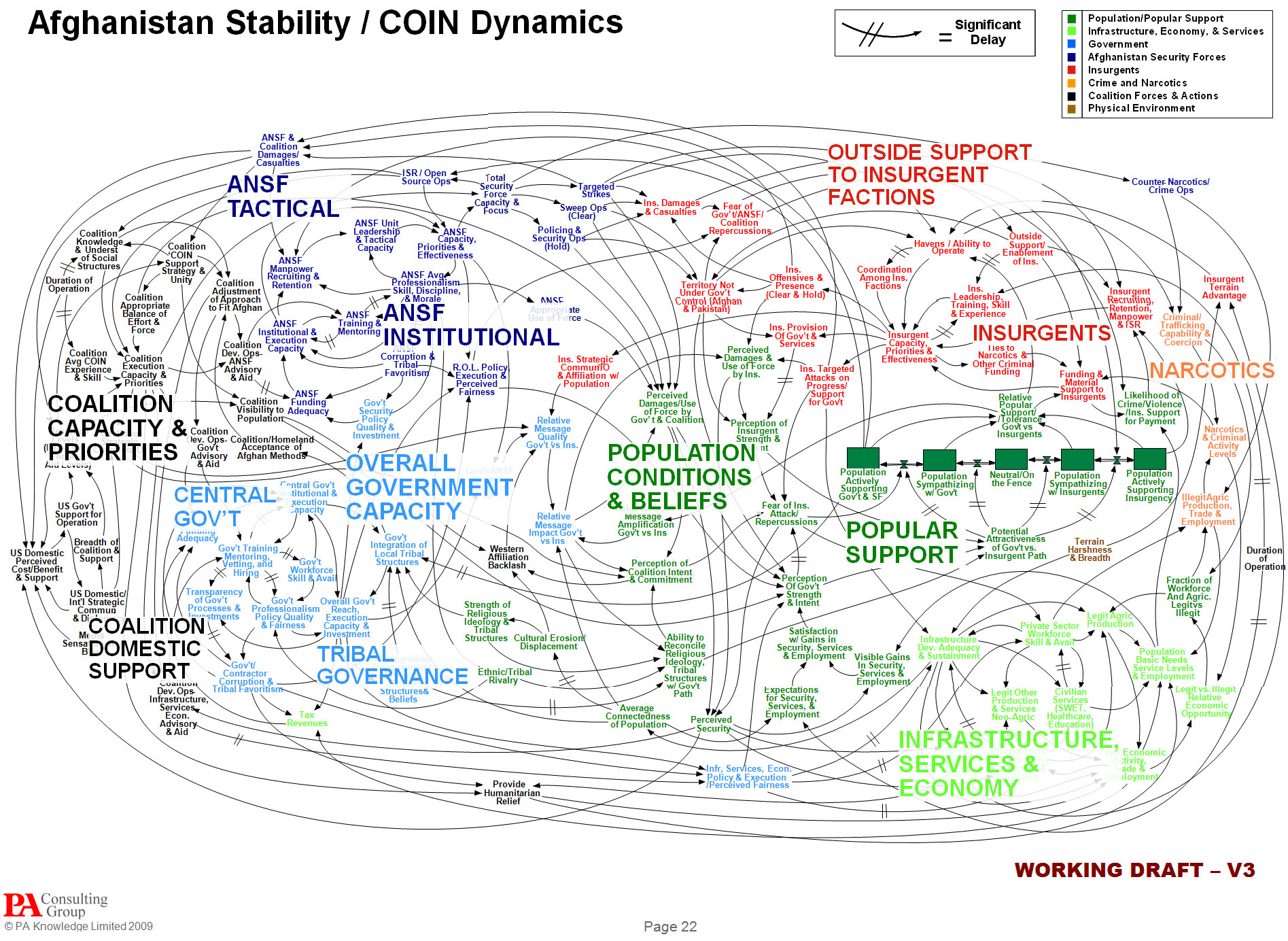
אחד התיאורים המפורסמים של שימוש בדיאגרמות משוב נוגע לשקף שכונה ״שקף הספגטי״ ותיאר את מכלול הגורמים המשפיעים על המצב באפגינסטן נוכח המערכה האמריקנית במדינה בעשור הראשון של המאה ה-21. הגנרל מק׳קריסטל שהוביל את המערכה צוטט כמי שטען כי ״כאשר נבין את השקף הזה ננצח את המלחמה״.
אם התוצאה של תיאור מפת הקשרים הוא ש״המציאות מורכבת״ יכול להיות שכדאי לחסוך את הזמן הנדרש לייצור המפה. כחלק מבעיות אלו, ד״ר צבי לניר טען כי בסוגיות אסטרטגיות לא פעם כדאי להמנע משימוש בקווים מאחר ובהגדרה כל המרכיבים קשורים אלו לאלו, וסימון הקשרים מפריע לנו מתיאור המתחים הכללים. לשיטתו, ההמשגות שלנו אודות הזיקות, המגמות והדפוסים במערכת חשובות יותר מאשר תיאור מעגלי המשוב הקונקרטיים:
|
חשיבה כזו מועילה מאוד כשמדובר במערכות מכאניות. גם כשאלה מורכבות מאוד. שלם שמורכב ממאות ואלפי חלקים, המקושרים ביניהם בקשרים לוגיים של לולאות משוב סיבתי. האבסורד בחשיבה זו בולט כאשר מנסים להפעילה גם לגבי מערכות חברתיות, שבמהותן הן מערכות סבוכות.[1] |
|
באותו אופן, דייב סנואדן, מנסח המודל של מסגרת קינפין התייחס בביטול לאפשרות לתאר דיגרמת משוב ברמת המערכת הרחבה:
|
|
Complex systems don’t have ‘causal feedback loops’ at a level that can mapped in the way you imply. Neither can you ever see the whole system. |
|
| – Dave Snowden, LinkdIn | ||
דוגמאות לדיגארמות משוב
דיאגרמת משוב הבוחנת צמיחה ודעיכה של חברת ביטוח
דיאגרמת משוב פשוטה הבוחנת את תחום האימוץ
דיאגרמה דינמית מתחום האימוץ
דיאגרמת משוב פשוטה על הקשר בין הכנסה ומאזן כספי בבנק
דיאגרמה בתחום אספקת המים
דיאגרמה הבוחנת מעורבות סטודנטים
.jpg)
כלים מקוונים המסייעים לייצר דיאגרמות משוב
לקריאה נוספת
- מפת ידע
- מפת הכוחות (causal loops diagram)– המבנה הסמוי של ארגונים מורכבים בתוך אתר אינטלגנציה ארגונית
הערות שוליים
- ↑ צבי לניר, פנקס הכיס של השועל, Kindle Locations 1955-1958.
תמונת הנושא מתארת דיגארמת CLD המתארת את הבעיות הסוררות בההתמודדות עם מגפת הקורונה, ומשותפת ברישיון CC-BY מאתר MDPI
יש שותפים רבים לכתיבה במאגר הידע. מאמר זה נכתב ברובו על ידי יותם הכהן. ניתן לצטט אותו באופן הבא:
- יותם הכהן, דיאגרמת משוב סיבתי (Causal Loop Diagram), מאגר הידע של דואלוג, 2021.
הטקסטים במאגר הידע מוגשים תחת רישיון CC-BY 4.0 וניתן לעשות בהם שימוש חופשי כל עוד ניתן קרדיט וקישור למקור.